Sphere Mesh Approximation Using SQEM Implementation

Last week we implemented a sphere-mesh algorithm using the Spherical Quadric Error Metric (SQEM) specified in Thiery et al.'s paper. The paper aims to provide a volumetric representation from a surface representation. The advantage of a sphere mesh is it allows better mobility of the object for animation. Thiery has also published a paper explaining how the SQEM approach can be used for animation.

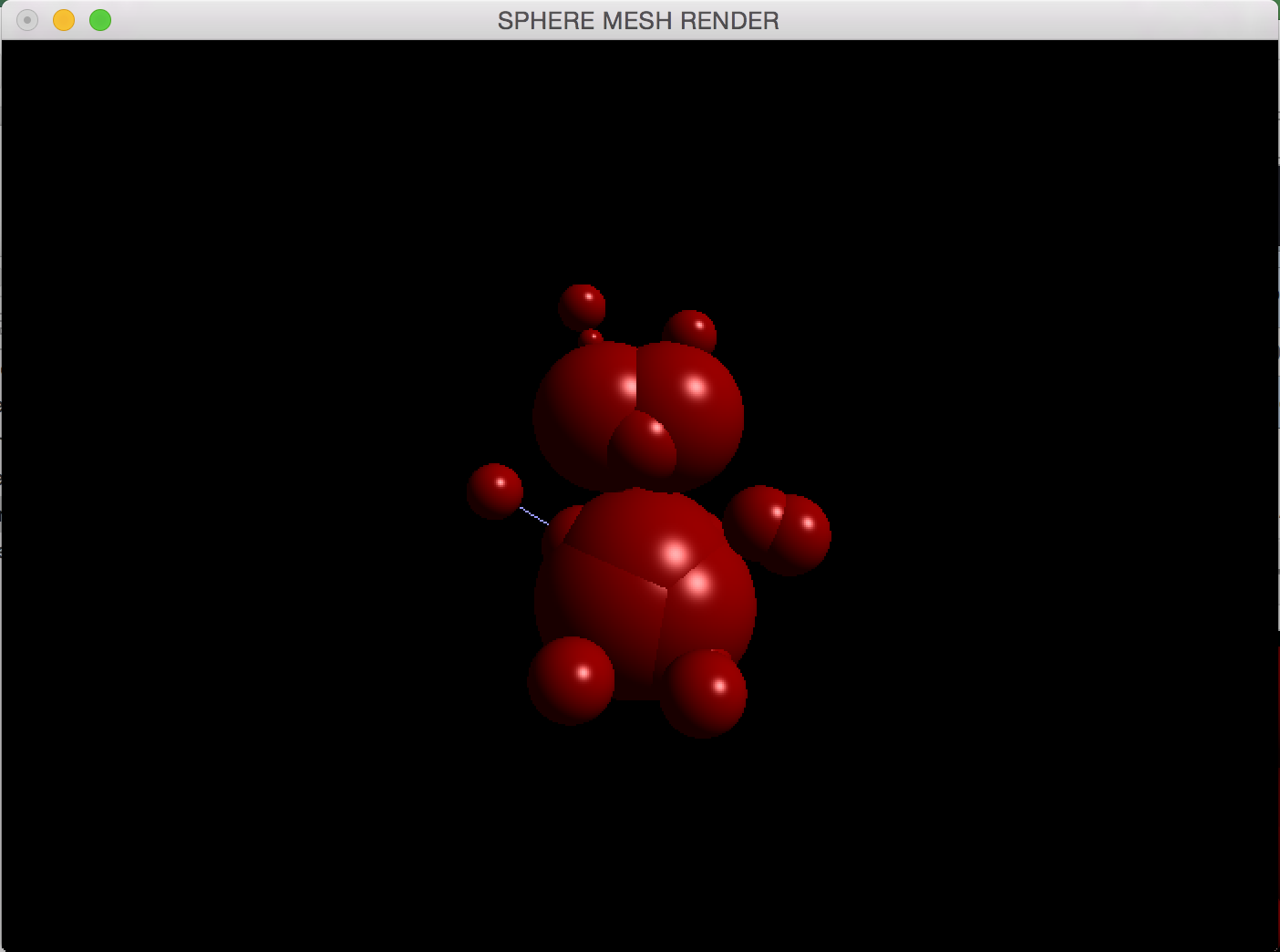
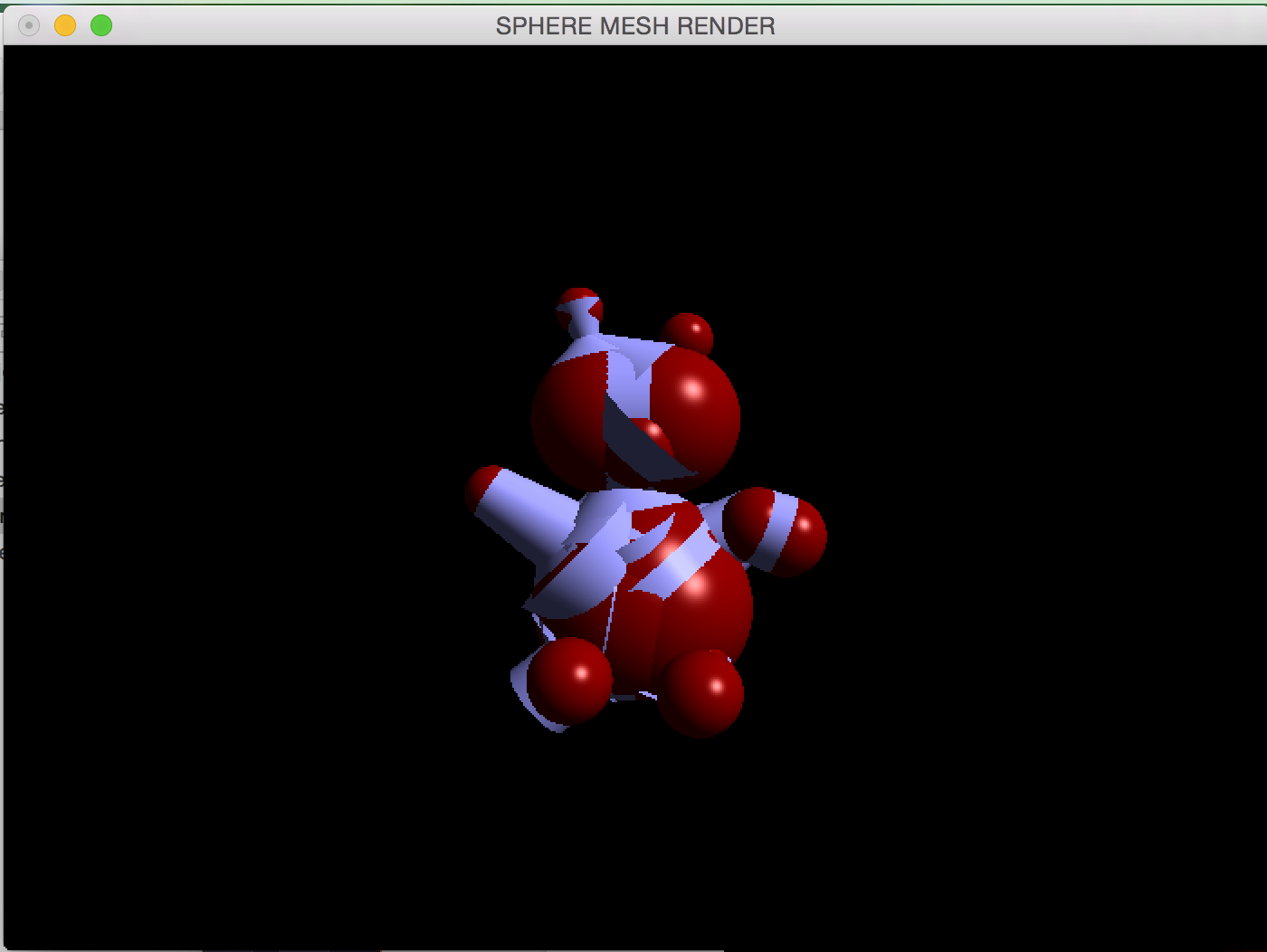
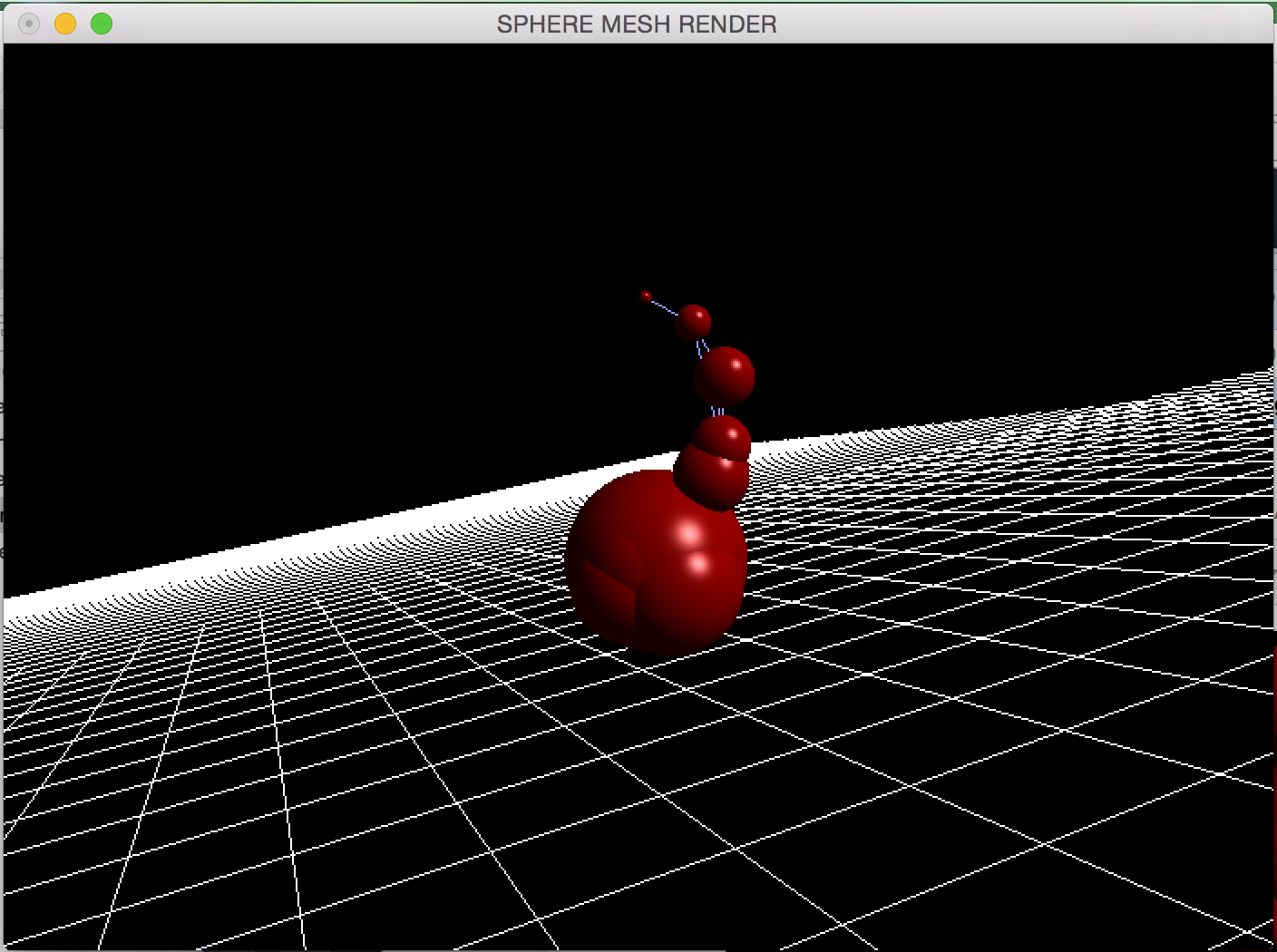
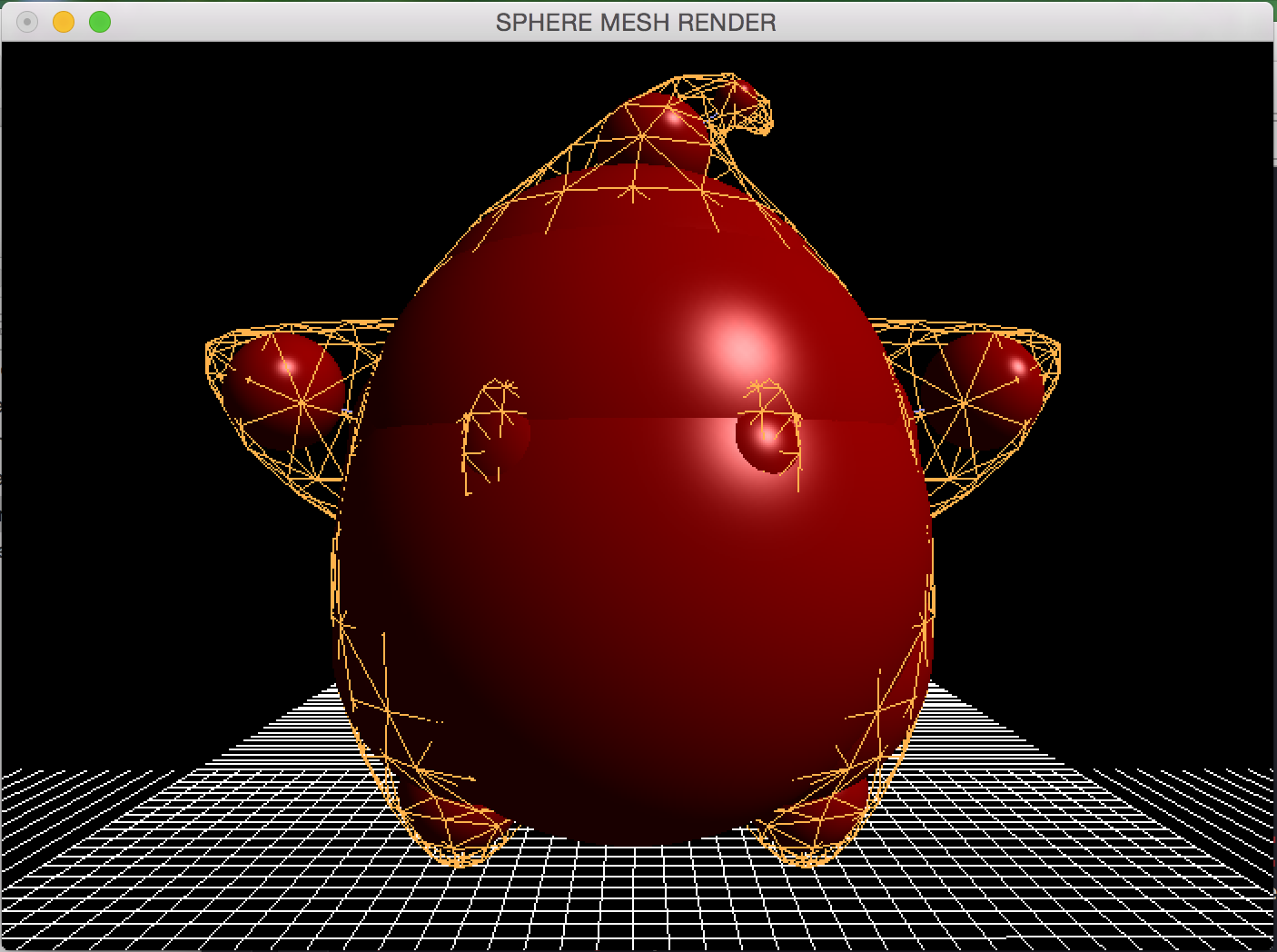
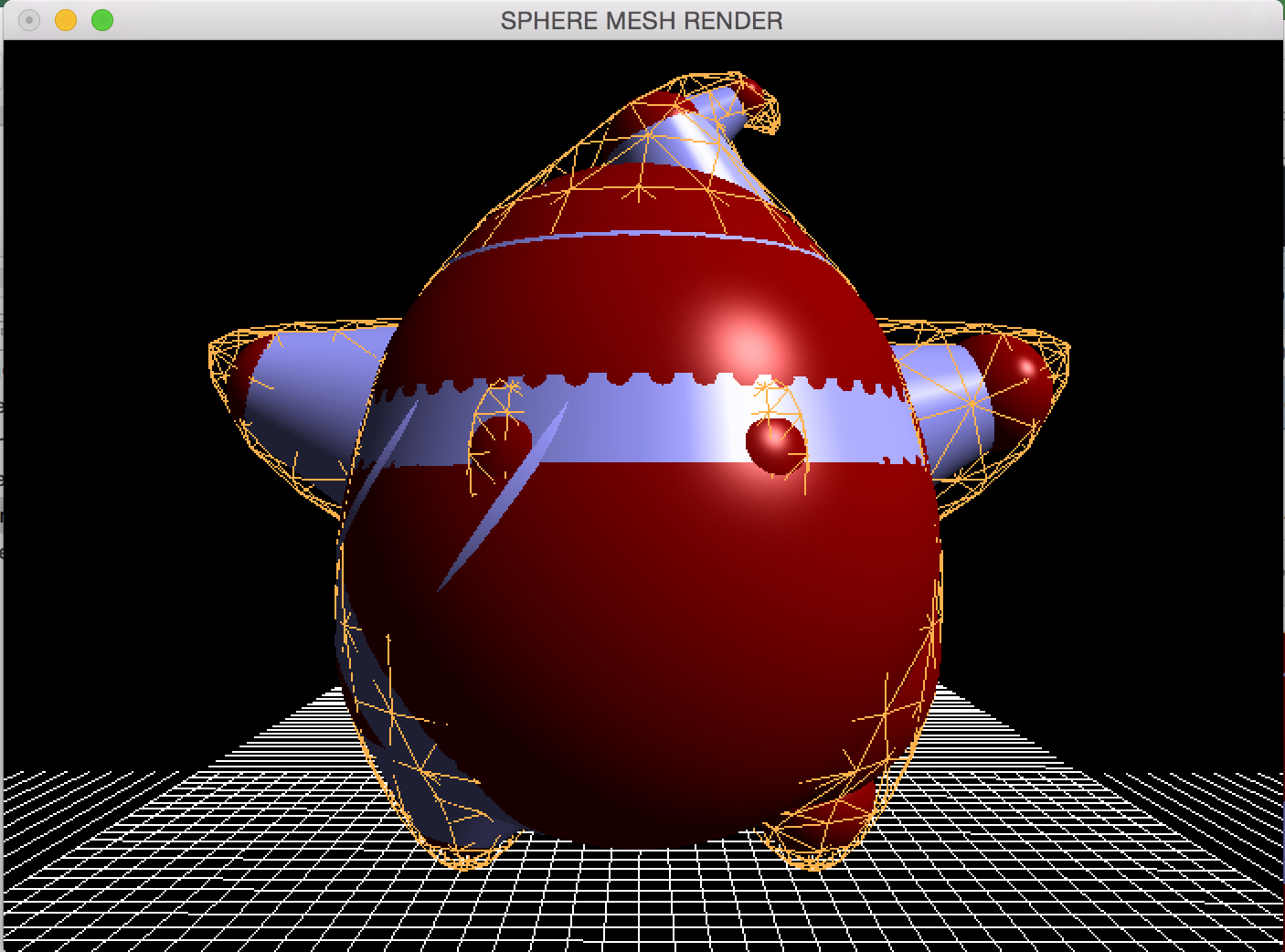
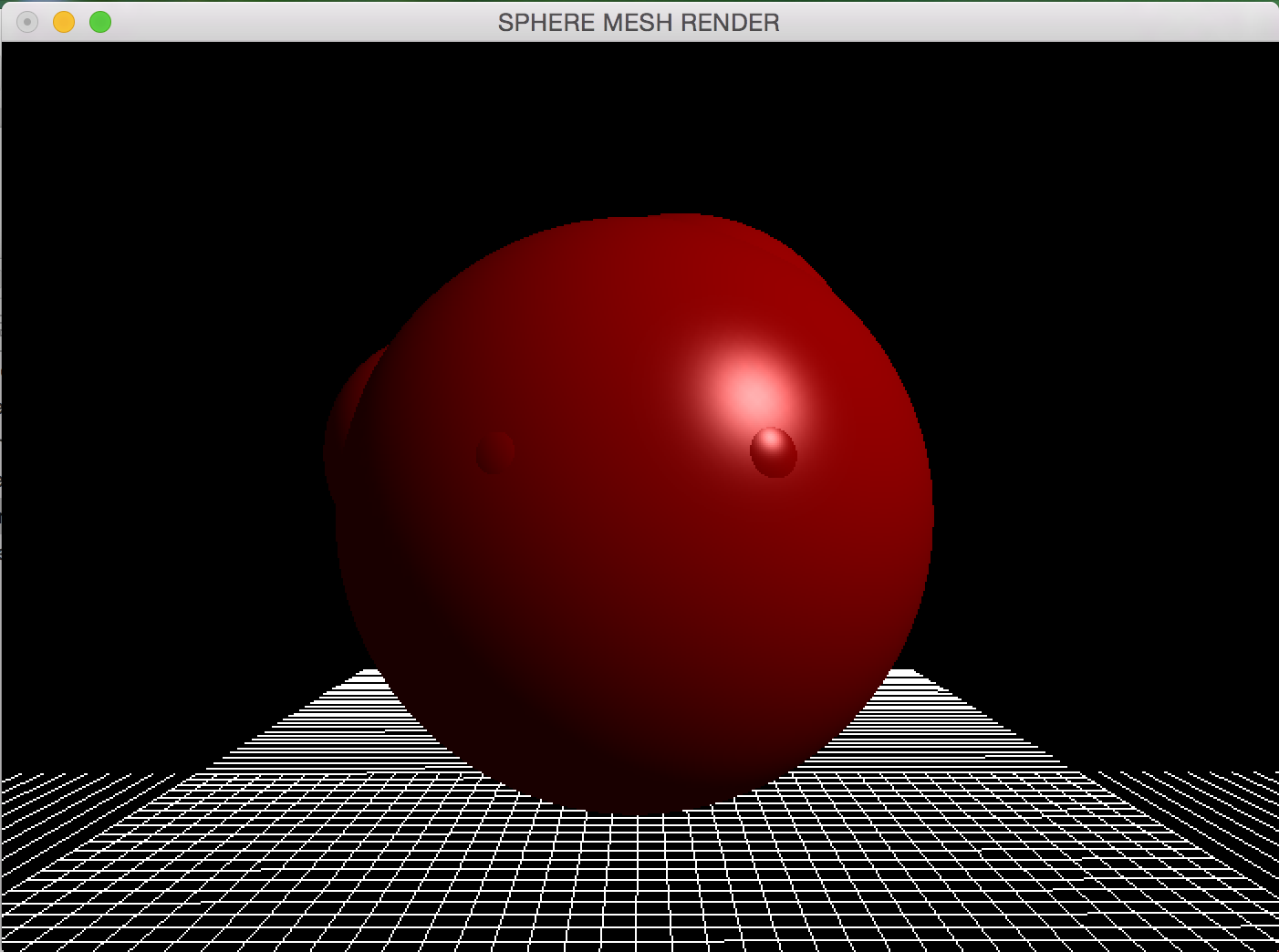
The above examples display the output of the algorithm with Luma.obj (first two images have 20 spheres whereas the last has 5 spheres).

The algorithm goes through a series of edge collapses (as most medial axis transforms and mesh simplifications go) on a triangulated mesh using Garland & Heckbert's greedy edge collapse method. The sphere mesh is represented as a series of 4D points (x, y, z, r) holding the center of the sphere and its radius. After collapsing edges of the triangulated input mesh, a quadric is created that approximated a given set for the edge collapses and generates a sphere that best approximates this area, essentially. After a series of calculations using the SQEM specified in the paper we get our best-fit sphere-mesh. The spheres are also interpolated (shown in image 2 above) with spliced cones.

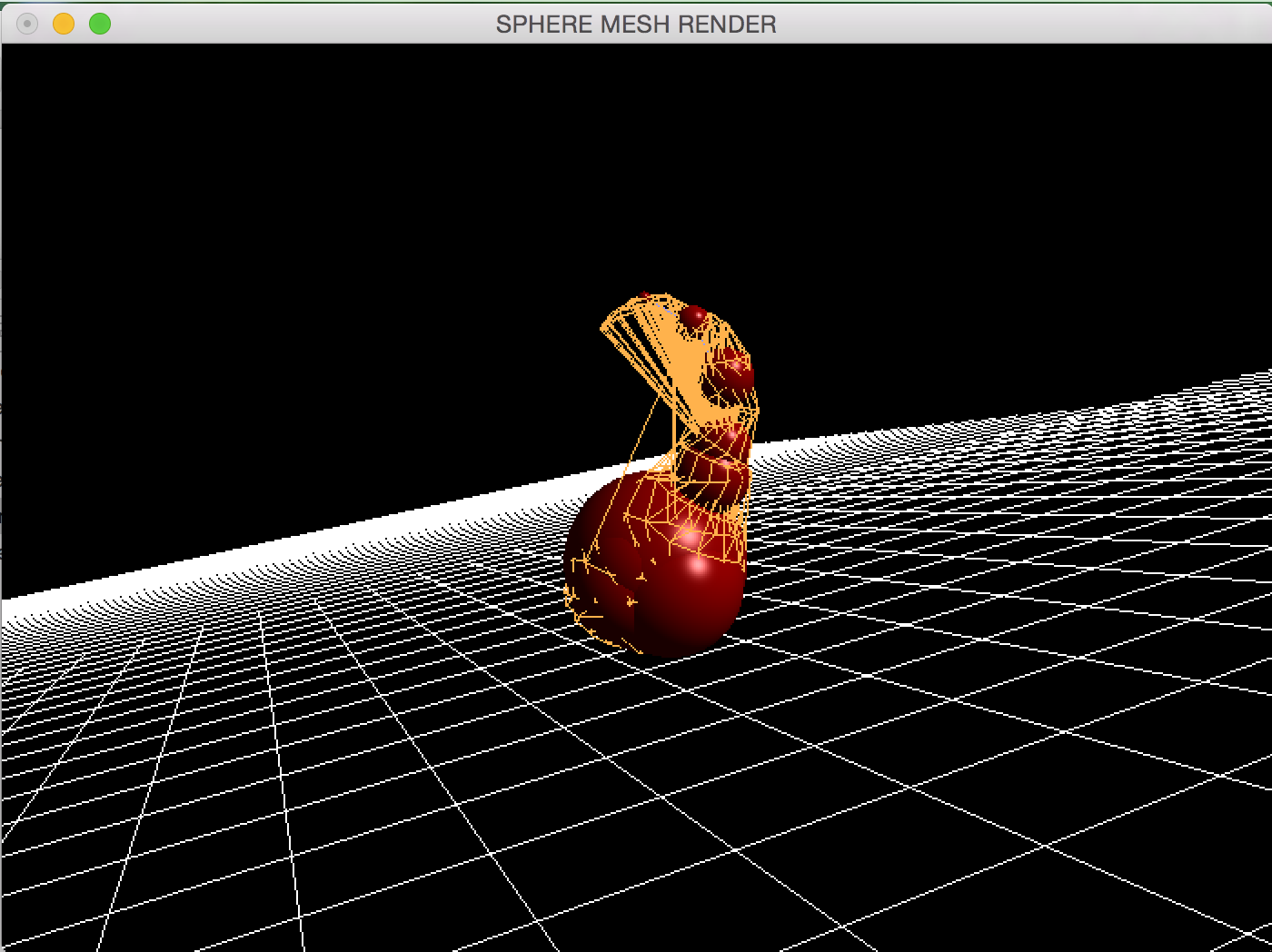
Below are more images using our implementation on Teddy.obj and gourd.obj files.